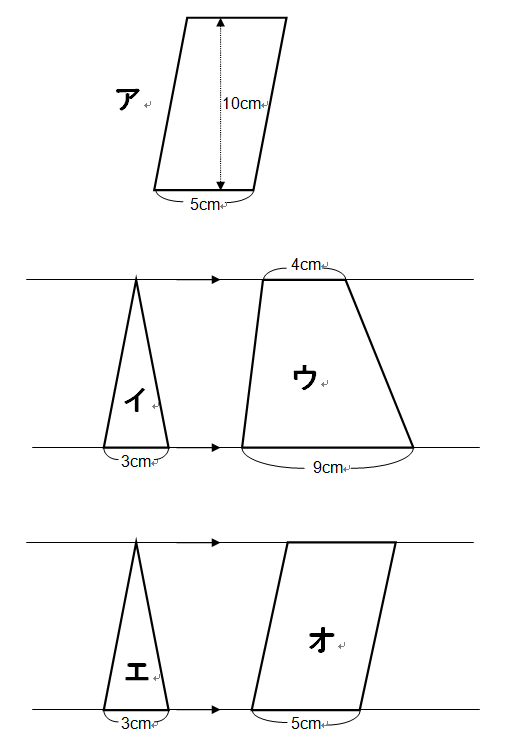
先生「平行四辺形でも台形の面積の公式が使えるのがわかるかな?」
生徒A 「???」
生徒B 「そんなバカな。」
生徒C 「平行四辺形も台形やもんな。」
生徒D 「じゃあ、台形も平行四辺形の公式が使えるのか。」
平行四辺形アの面積は5×10=50と求めますが、「上底と下底がたまたま等しい台形」とみなして(5+5)×10÷2=50でも求めることができます。平行四辺形は台形の条件を満たしているからです。逆に台形は平行四辺形の条件を満たしていないので生徒Dの言っていることはもちろんペケ。
このような発想は単に面積を求めるだけなら必要ありませんが、面積比の問題になると大きな差となって現れます。イとウの面積比は3:(4+9)=3:13と言えても、エとオになると3:(5+5)=3:10と言えない(迷っている)生徒がたくさん出てきます。
[対策]
だいだいは生徒Aや生徒Bのような反応をしますが、このような話をどこかで聞いた時に、実際に自分で試しておくこと(簡単に試せることです)。
ちなみに、三角形も「たまたま上底が0の台形」とみなして面積を比べることもできますよ。